수많은 파라미터를 가지고 있는 인공지능 모델에서 compression 압축하는 기법은 매우 중요하다.
Model Compression 기법에는 Pruning 가지치기, Quantization 양자화, Knowledge Distillation 지식 증류 등이 있다.
https://suhyeonlee.tistory.com/2
[ML] 모델 경량화 방법 3가지: Pruning, Weight Quantization, Low-Rank Matrix/Tensor Decomposition
from "Deep neural networks compression: A comparative survey and choice recommendations" IntroDNN은 하드웨어와 대규모 데이터셋의 발전으로 image processing, financial forecasting 등의 문제를 이전보다 잘 해결하고
suhyeonlee.tistory.com
Segmentation Anything Model(SAM)은 Meta에서 만든 획기적인 segmentation model이며 성능이 매우 좋다.
다양한 Variant 연구들이 진행되고 있는데 저번에는 Knowledge Distillation을 적용한 SAM 중에서도 EdgeSAM을 알아보았다.
오늘은 Quantization을 적용한 PTQ4SAM을 알아보고자 한다.
PTQ4SAM

PTQ와 QAT의 가장 큰 차이는 말 그대로 training 동안 양자화하는 건지, training 후에 양자화하는 지에 있다.
PTQ는 훈련이 끝나고 양자화를 한다.
따라서 전체 훈련 데이터셋이 필요없고 양자화를 하기 위한 range 파악을 위해 small unlabeled samples가 필요하다.
굳이 labeled일 필요가 없는 것은 label로 loss 계산을 하는게 아니고 activations range만 보기 때문이다. QAT는 forwarding/backwarding에서 quantization loss를 학습한다.
두 가지 문제를 살펴보자.
Bimodal Distribution 문제 -> BIG로 해결

post-Key-Linear이란 attention 계산을 위한 query, key 를 만들어낼 때 거치는 linear layer이다.
attention의 매커니즘은 linear -> dot-product (attention score) -> softmax -> weighted sum 이다.
연구진들은 key용 linear layer를 통과한 activations들이 쌍봉분포를 보임을 확인했다.
이 쌍봉분포는 tensor-wise하게 보면 나타나는데 channel-wise로 보니 channel의 반은 양의 봉우리에, channel의 반은 음의 봉우리에 치우쳐져 있었다.
이 쌍봉분포가 문제가 되는 이유는 양자화할 때 분포를 잘 파악하는 게 중요하기 때문이다.
양자화할 때는 보통 max, min를 따져 range를 가져오는데 쌍봉분포에서는 이런 range가 실제의 분포 이상으로 넓게 가져와지고 그림 (a)에서 처럼 actiavations가 없는 void한 부분이 있는데도 이 범위가 포함되게 된다.
연구진들은 이 문제를 BIG로 해결한다.
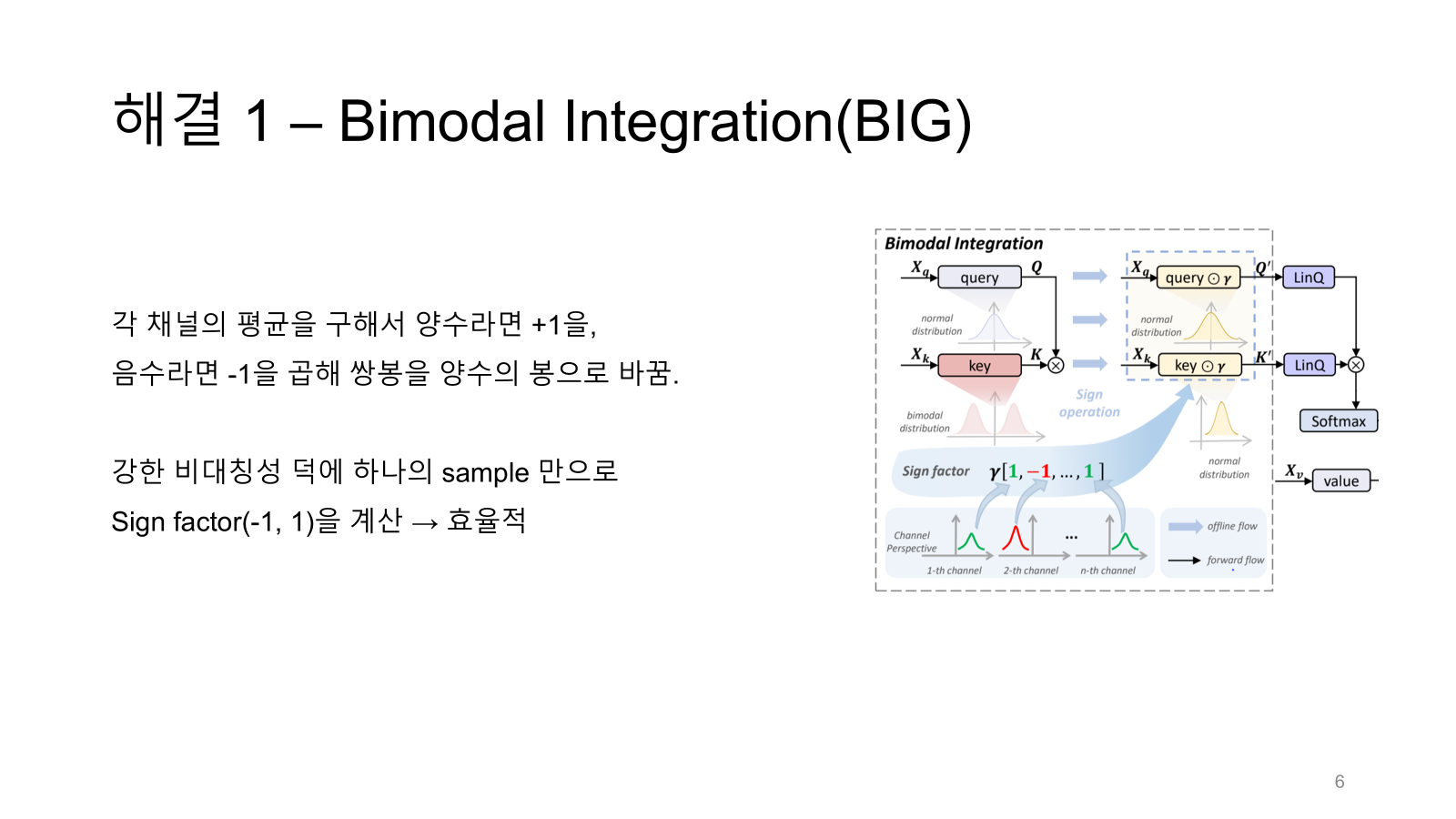
먼저 key linear 채널별로 양수나 음수쪽에 값이 치우친다고 했으니까 각각의 채널마다 평균을 구해서 양수인지 음수인지 파악한다.
그리고 양수면 sign factor r에 1을 음수면 -1을 할당한다.
그리고 그 채널과 sign factor를 곱하면 tensor-wise로 봤을 때 쌍봉이 아닌 normal 분포가 나오게 될 것이다.
다만 equivialent transformation이 될 수 있도록 key linear layer뿐만이 아니라 query linear layer에도 sign factor를 곱해준다.
이게 무슨 말이냐?
attention score를 구할 때 $QK^T$ 즉 내적값을 구해야하는데 key 즉 K에 -1을 곱하면 값이 음수가 되어버린다.
값은 유지시켜주기 위해 즉 equivalent 등가적으로 transform 변형해주기 위해 key랑 query 둘 다에 곱해주는 것이다.
오른쪽 그림을 보면 r을 query와 key에 둘 다 곱하고 있다.
결론적으로 $QK^T$ 의 값 변화는 없지만 key의 쌍봉 문제는 해결되었다.

모든 linear activations가 쌍봉 분포를 띄는 건 아니다. 따라서 쌍봉 분포를 찾아내는 것이 관건이다.
여기서 Gaussian KDE를 사용하는데 KDE에서 자주쓰이는 메소드 중 하나이다.
KDE는 discrete한 값들을 continuous 하고 smooth하게 바꿔주는 함수이다. (사진 출처 위키피디아)
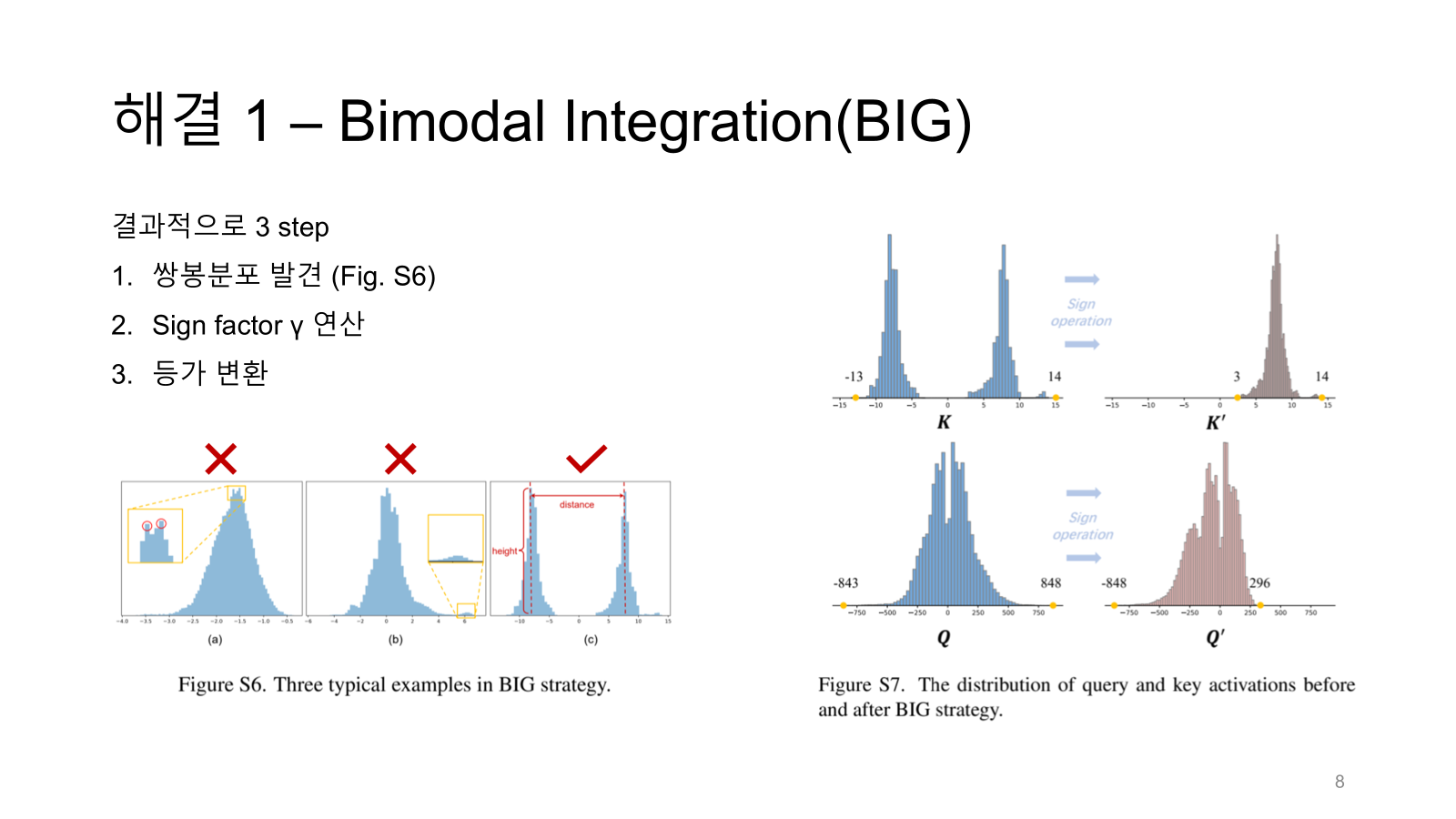
이 쌍봉분포를 어떻게 알아내느냐?
Figure S6 (c)를 보면 height, distance가 표시되어있다. 이 두 조건을 threshold 삼아 우리가 찾고자 하는 쌍봉이 아닌지 판별한다.
예를 들어 첫번째 그래프는 작은 봉 두 개가 보이지만 distance와 height가 너무 작고 두 번째 그래프에서 두 봉우리는 height가 달라 비대칭적이다.
1,2,3 스텝을 완료하면 오른쪽 그림처럼 K와 Q 분포 변화를 볼 수 있다.
K의 쌍봉은 사라졌으면 (-13~14) 이던 range가 (3, 14)로 바뀌었으며 Q도 range가 변했다.
그럼 이제 두 번째 문제를 address해보자.
분포의 다양성 문제 -> AGQ로 해결

attention 매커니즘의 softmax는 innate하게 power-law 문제를 지닌다.
즉 지수함수적 특성을 지녀 몇몇 요소는 큰 값을 갖고 나머지 다수는 아주 작은 값으로 분포한다.
기존 연구들은 -self-attention softmax에 특화된 quantizer를 제시하는데 SAM의 경우 두 cross-attention과 self-attention을 사용한다.
두 개의 cross는 token-to-image랑 image-to-token이다.
그러다 보니 이 세 개의 attention의 분포도 다양하게 나타나 하나의 quantizer만으로는 해결하기가 어려워 이 연구에서는 adaptive하게 granularity를 조절하는 quantization을 제시한다.

일단 중간에 있는 식이 quantization 수식이다.
로그 함수를 포함해 power-law를 완화한다.
또한 파라미터 타우를 넣어서 타우가 클 때는 큰 값 분포를 가지는 attention(위 슬라이드에서 image-to-token 분포)를 fine-grained하게 바꾸고 타우가 작을 때는 작은 값 분포(token-to)를 fine-grained하게 바꿔준다.
dequantization 식은 quantization 역연산인데 보면 2의 지수부분이 분모를 타우로 가지면서 정수가 아니게된다.
하지만 효율적으로 bit-shifting을 하려면 정수가 필요하다.

여기서는 bit-shifting을 할 수 있는 방법을 제시한다.
먼저 2의 지수부분을 정수부와 소수부로 나눈다.
그리고 score와 value값을 곱한 식으로 생각을 해보면 소수부분을 가진 부분을 빼면 bit-shifting이 가능하다.
소수부분도 결국엔 타우의 개수만 필요하므로 LUT를 만들어 쉽게 소수 부분을 연산을 쉽게 할 수 있도록 한다.
대략 4KB로 매우 가볍다.
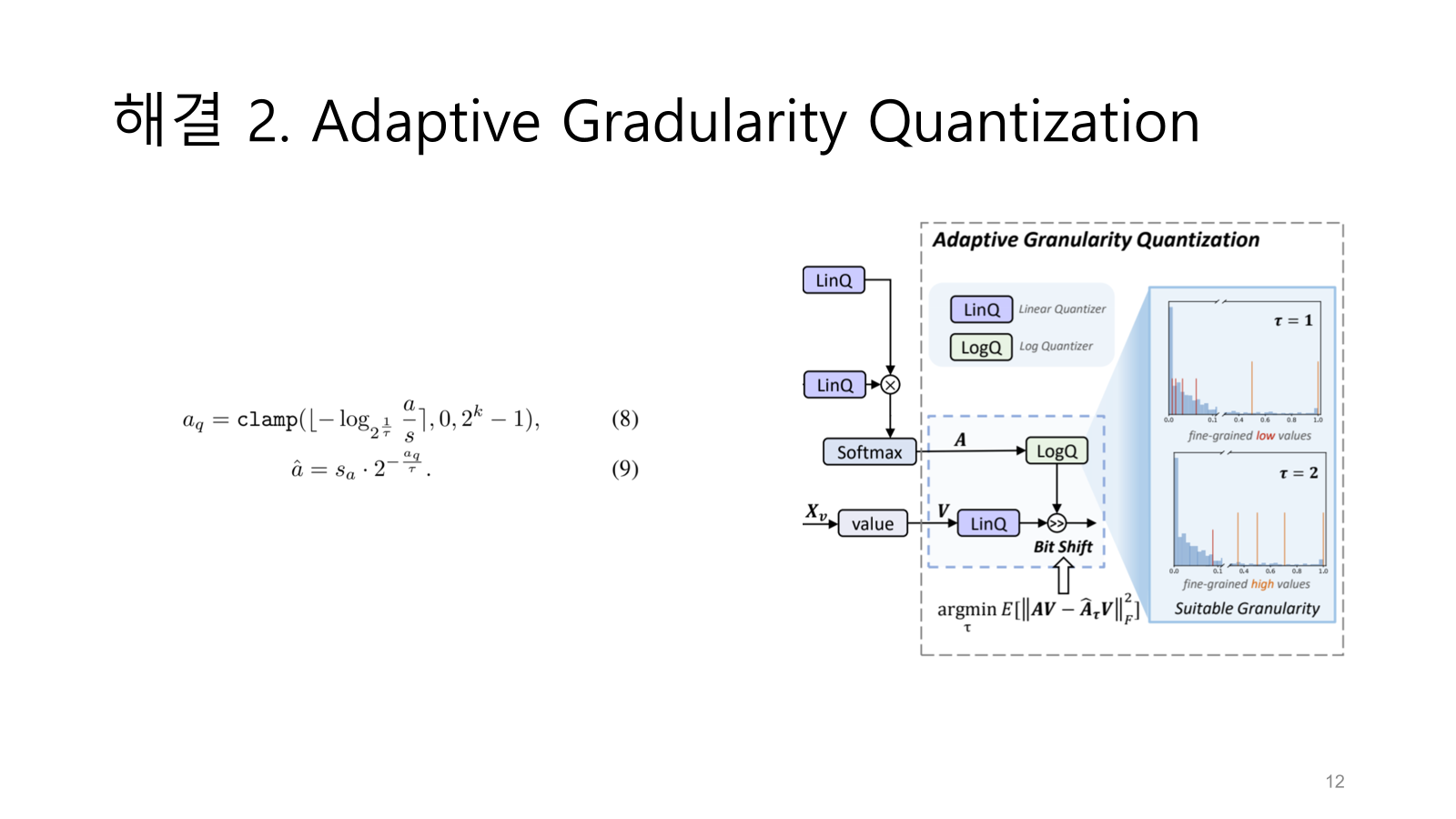
논문에서는 linQ와 logQ로 타우와 log가 포함된 quantizer를 정리한다.
아래 argmin 계산으로 적절한 타우를 찾아낸다.
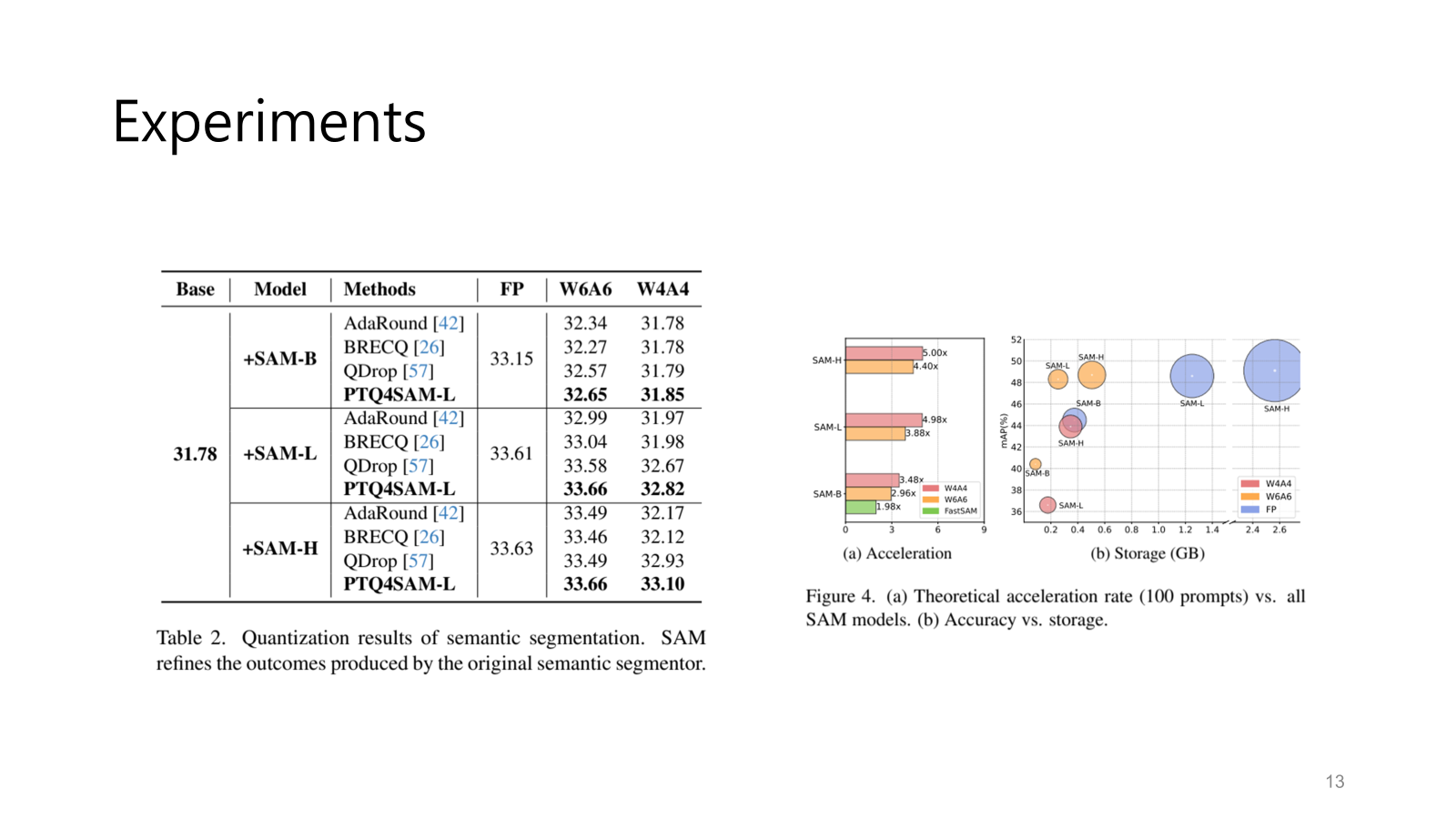
semantic segmenation, image segmentation, object detection 등 여러 방면에서 성능이 좋음을 보였고
비교군은 다른 quantization 방식인 AdaRound, BRECQ, QDrop 등이다.
무엇보다 경량화니까 acceleration과 storage도 따져보아야 한다.
속도는 3배에서 5배까지 빨라질 수 있고 정확도가 유지되는 선에서 용량은 몇 배는 가벼워질 수 있다.